Other articles by Alex Stuart

How the Jump Button Works

I once wrote a letter to Nintendo Power magazine, naïvely asking how games were made. A few weeks later I got a letter back—can you imagine that today? It was friendly and provided some information about the whole production process, but I was slightly disappointed. I still didn’t know how the buttons worked.

You know, the buttons on the controller, the ones that let you participate in an oneiric cocktail of colors, triumphs, and thumping basslines like Sonic the Hedgehog. While I heard that the movie adaptation starring Jim Carrey was surprisingly good, it just can’t live up to playing that game. The magic is in the buttons, and my pen pal at Nintendo Power was mum about it.

In Sonic it goes like this: when you press the left or right side of the directional pad Sonic starts running left or right, picking up speed the longer you press. Press on the bottom side, and he curls up into a ball like a hedgehog—if he’s already running, he starts rolling. Finally, you press a trigger button to make him jump into the air.

Not too complicated, especially compared to more modern extravaganzas. But describing even that simple scheme requires a lot of hypotheticals: when and if and the longer you press. By the same token, there’s an assumption of causation: the button makes Sonic jump. How do these things work?

Not always magical

The short and honest explanation of how the jump button works is however it must work. There’s a better explanation, but first the ugly realities of game programming demand some acknowledgement. The moment someone decides that there should be a jump button, some kind of computer system exists that constrains what that can mean.

It might be nothing more than a machine, or an operating system, or a programming language. Or it could be a framework, or a game engine, or a tangle of legacy code. Whatever it is will define the technique a programmer uses to implement the jump button or any other feature.

Great studios develop their software to support tools that enable a natural implementation for certain kinds of new features. But even great tools don’t usually cover all of the eventual design. In these cases, the expedient solution is to use the tools (scripts/engine/language) in unintended ways. These ways are frequently also unintelligible and unreliable. ¹

So, more precise descriptions of how jump buttons work will vary a lot between different games, and they’re liable to be discouraging stories of arbitrary trials and random success. Most people would rather learn something useful for improving their own lot. What if there were some theory of jump buttons that could shed light not only on all of the existing implementations, but on any new implementation as well?

Boy, that would be really nice! —Kris Sikorski

What jumping means

A theory is based on definitions, and to explain the jump button we have to define what jumping means. Anyone who played these games growing up as much as I did will be tempted to say, well, he jumps off the ground and into the air, anything else? What jumping means in a video game might seem as obvious as what it means in real life.

Neither is actually obvious, though thankfully a game can be a lot simpler to explain than the physics of the world at large. Let’s start with that seemingly obvious definition anyway, because it contains a valuable insight: when Sonic jumps, he was on the ground and then he’s in the air. Jumping is a sudden transition to a very different part of the game process.

In the first part, Sonic is moving left or right, but not up or down. The directional pad determines his acceleration, up to a maximum running speed. This could go on indefinitely, but it will end when the jump button is pressed.

In the second part, Sonic is moving in some kind of arc, upwards at first but accelerating downwards as if by gravity. He might be moving left or right too; the directional pad determines some mid-air acceleration, but not as much as before. Here, though, there is no restriction on his speed. This part is always temporary: it ends when he reaches the ground. ²

There are more differences between these two parts than just how Sonic moves. On the ground he has standing, running, and toe-tapping sprite animations, and he can get hurt if he touches an enemy. After he jumps he starts to spin, so he has spinning animations and can destroy most enemies he touches. A sound effect begins playing back, too. All of these changes occur at once, and we call that jumping. Somehow, the jump button causes all this to happen.

Continuous and unified

Physics would try to describe these two parts of the game with one minimal set of laws that apply continously, at all times. Then either part would be a special case of the single, unified phenomenon. For example, we could say that gravity always causes a downward acceleration. That would shape the arc of the jump and bring Sonic back toward the ground. Then, to make sure he stops when he reaches the ground, we could say that the ground exerts an equal and opposite force on anything it touches. The jump button, then, would apply a short upward force to launch Sonic into the air.

Some of Sonic the Hedgehog would emerge from this one set of laws, but not all of it. For one, we’d need an extra law to say that the jump button only works when Sonic is touching the ground: otherwise, he’d be able to jump over and over again in mid-air. Similarly, we’d need an extra law saying the horizontal acceleration is different in the air than on the ground. We also want Sonic to stay right on top of the ground, rather than sinking into it. The process can’t determine Sonic’s contact with the ground until after it happens, so he would come to a stop knee-deep in dirt. We’d need an extra force not just counteracting gravity but actually pushing Sonic out of the ground when he’s partially inside it.

Already the nice, unified theory demands a lot of extra complexity. We began with almost no hypotheticals, but we had to add them in anyway—even before we’ve addressed sprite animations and interactions with enemies. What would coding this look like?

A unified program

Imagine one big while loop that computes all the changes in the game over successive intervals of time:

while (true) {
    // compute the next step of the game
    ...

The body of the loop encodes one set of laws that govern these changes.

Sonic’s location p and his velocity v represent the state of his motion. p always changes as the integral of v over time dt.

    p = p + dt * v;

Gravity always causes a constant downward acceleration, integrated over time and added to v.

    v = v + gravityAccel * dt;

Horizontal acceleration is proportional to dpad, the state of the directional pad, but unlike gravity the proportion is not constant. It depends on whether Sonic is on the ground or not. A variable sonicOnGround keeps track of that.

    if (sonicOnGround == false) {
        v = v + dpad.x * airAccel * dt;
    }
    else {
        v = v + dpad.x * groundAccel * dt;

Because they only apply on the ground, four other rules appear in this else block:

1. the gravitational reaction force from the ground;

        v = v - gravityAccel * dt;

2. the repulsion force to keep Sonic on top of the ground, which is proportional to how much less his vertical location is than the height of the ground at his horizontal location;

        v = v + (p.y - ground(p.x)) * repulseAccel * dt;

3. the jumping force, which furthermore only applies when trigger, the state of the jump button, indicates that the button is pressed;

        if (trigger) {
            v = v + jumpAccel * dt;
        }

4. finally, the speed limit.

        v = speedLimit(v, maxSpeed);
    }

So much for acceleration. Now the process needs to determine whether Sonic is on the ground. Remember, this determination must always happen the same way, regardless of whether he is actually on the ground or not. It is a comparison of his elevation with the height of the ground at his horizontal location.

    if (p.y > ground(p.x)) {
        sonicOnGround = false;
    }
    else {
        sonicOnGround = true;
    }
}

Ta-da! Did you catch how the jump button works? It’s up there in the statement that begins with if (trigger). The button opens a branch in the main loop that adds an upward acceleration to Sonic’s velocity v. The next time around the loop, that information reaches the location variable p via integration from v. At that point p should be high enough vertically to open the else branch of the ground height conditional, which assigns sonicOnGround the value true. Then the next time around the loop, the jumping effect is fully observable.

Unified, except where it isn’t

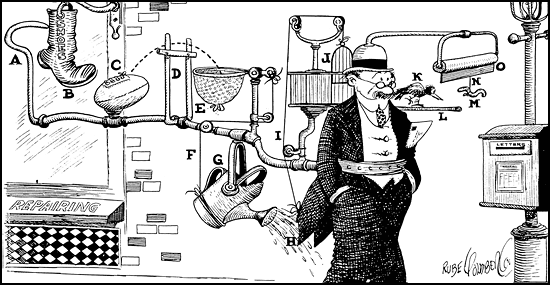
Like physicists, we attempted to reduce the total complexity of explaining everything by eschewing simpler but incompatible explanations of individual things. And the forces are indeed nice to think about: we can add them in any order; gravity is always there just as in real life. But this handful of simple forces is not enough to model jumping. To fill in the rest of the model we also used the control structures of our programming language. The model is thus a linkage of unrelated devices like a Rube Goldberg cartoon.

That subverts our assumption that the model is unified, and we have no warning besides indentation. Oh, you thought this law always applies? Sorry, you missed the if statement so many lines above this one. For example, the conditional repulsion force amounts to a trampoline that makes Sonic oscillate between standing and jumping like a glitch in Super Mario 64. But our model is supposed to be continuous and unified, so in principle any part of it could cause the same behavior. To fix it, someone would have to infer that the cause is a discrete exception to the continuous rule and then find whatever that might be, conditional branch or not.

Finding it becomes more difficult the more features we add. Encoding the sprite animations, enemy interactions, and sound effects in this program would lengthen each branch of the conditional—or worse, introduce new conditionals later in the loop body. Like the motion, each of these features is split into two parts, one for the ground and one for the air. They will all further subvert our fiction of a unified model in increasingly unpredictable places.

On top of that, the ground motion and air motion aren’t even the only discrete phases of the game. The unified program will need more flag variables like sonicOnGround. Some will further gate the execution of one or the other of the existing branches; for example, a flag for whether Sonic is rolling will disable the running-acceleration on the ground. Others will gate the execution of the whole conditional; for example, a flag for Sonic being in a Special Stage will disable both ground and air motion and enable other, special rules of motion.

These exceptions are going to make mincemeat out of any consistency we think this program has. But if not in spirit, then at least in principle: we’ll still have that big while loop unifying everything. Great.

☙

Discrete pieces of continuity

By now it’s clear that our unified, continuous model of jumping isn’t really continuous. And it shouldn’t be, because we established that jumping itself isn’t really continuous. It’s a discrete transition between two different parts of the game. Each part might be continuous on its own, but any continuous model of one is not necessarily a good model of the other.

For example, we might say that there is no gravity when Sonic is on the ground. Why not? There’s no need to explain his vertical acceleration, because he has none. Moreover, his vertical velocity is zero too. Why not forgo integrating vertical velocity at all? Instead, we just say that his vertical location is identical to the ground height at his horizontal location.

Conversely, we can mostly ignore the ground when Sonic is in the air: no reaction or repulsion forces, and no jumping. We only consider the ground to determine the moment that Sonic touches it—the moment the air model no longer applies.

The jump button, then, is a part of the ground model only. All it needs to do is cause the air model to take over: it just needs to transfer control of the machine between two separate sections of the program.

A two-loop program

Imagine two while loops, one for each model. Each loop begins via a function call and runs forever—until it’s time to switch to the other. Another while loop links these calls together, so the exit from one is the entrance to the other.

while (true) {
    groundLoop();
    airLoop();
}

As soon as the ground loop terminates, the air loop begins; when that terminates, the ground loop begins again.

Rather than track location and velocity in two dimensions, groundLoop tracks only horizontal location x and horizontal speed s. It does this by calling a function groundMotion. As before, x varies as the integral of s over time.

void groundMotion() {
    x = x + s * dt;

As before, s depends on dpad (now groundAccel is one-dimensional), and it has a speed limit. But since we’re only considering the ground case, those things don’t require a conditional branch. It’s just simple, straight-line code.

    s = s + dpad.x * groundAccel * dt;
    s = clamp(s, -maxSpeed, maxSpeed);
}

That’s it for motion on the ground! There’s no variable for vertical location, because that is always given by the expression ground(x).

Motion in the air, on the other hand, really is two-dimensional. So airLoop calls a function airMotion that tracks both location p and velocity v in two dimensions, just as the unifed program did.

void airMotion() {
    p = p + dt * v;

It always applies gravitational acceleration, because in this loop, always means when in the air. Accordingly, it always applies the mid-air acceleration too.

    v = v + gravityAccel * dt;
    v = v + dpad.x * airAccel * dt;
}

That’s it for motion in the air! This case too requires no conditional statements.

Before entering the loops that call these functions, groundLoop and airLoop each initialize their state variables based on the values of the other loop’s variables. The ground loop’s horizontal location x and speed s receive the values of their counterparts p.x and v.x in the air loop.

void groundLoop() {
    x = p.x;
    s = v.x;
    while (true) {
        groundMotion();

After computing its motion, each loop also checks its exit condition. On the ground, this is just trigger, the state of the jump button.

        if (trigger) {
            return;
        }
    }
}

So, in this program the jump button works more directly than in the unified program. It opens a branch that just leads directly to the air loop itself; the information from the button goes straight into our programming language’s internal control mechanism.

Initializing the air loop is more involved because it has more variables. The two-dimensional location x receives the ground loop’s current horizontal location x and the current ground height given by ground(x). Velocity v is initialized with the ground loop’s current horizontal speed s and the constant jumpImpulse, the initial vertical velocity during a jump.

void airLoop() {
    p.x = x;
    p.y = ground(x);
    v.x = s;
    v.y = jumpImpulse;
    while (true) {
        airMotion();

The air loop checks its exit condition with the ground height comparison.

        if (p.y <= ground(p.x)) {
            return;
        }
    }
}

This two-loop program is unconventional. Nevertheless, it encodes our definition of jumping in a more straightforward way than the unified program does. It doesn’t rely on the latter’s unstable repulsion force, meaning that Sonic will be stable on the ground as we expect him to be. More importantly, it replaces conditional behaviors in the unified model with the unconditional behavior of two separate models. This way it is clearer how and when the two behaviors interact—and crucially, that they aren’t messing each other up. In exchange for these virtues, we lose only the temptation to pretend that both behaviors follow one and the same set of rules. It’s a little too good to be true.

You gotta keep ’em separated

Unfortunately, to any user of C or its derivatives like Python or JavaScript, the two-loop program looks like an unrealistic cartoon based on the tacit assumption that we can somehow run nested, infinite while loops.

Absent some concurrency mechanism, no other code ever runs. If there is only one thread of execution, code for things like drawing, sound, sprite animation, enemy motion, and indeed everything else in the game would have to be part of (or called from) the loops for Sonic’s motion. They can’t be anywhere else, because any code not linked to these loops is forever unreachable!

That would quickly become a mess. Can you imagine groundMotion extending for thousands of lines, updating not just Sonic’s motion state but also enemies’ motion states, and their entrances and exits, and their sprite animations? It might include unique drawing commands to draw Sonic at ground height, whereas airMotion would have different drawing commands to draw Sonic at any height. The loops would lose their association with Sonic’s motion, becoming amorphous, top-level control code.

Maybe that would make sense if the entire game were neatly divided into a ground mode and an air mode. But again, these are not the only discrete phases of the game. We could not use this same technique to simplify other mode transitions, like an enemy changing its attack pattern. It would require even more nested loops that include code for every feature, and it would be ambiguous which one should be in control. This is not just messy but actually unmanageable. Instead, these other mode transitions would have to be conditional branches gated by flag variables, just as they were in the unified program.

Well, that sucks! Nicely separating Sonic’s motion into two loops gains us almost nothing in the scheme of organizing the whole game. What good is a clean jump button that makes everything else into a train wreck?

Beyond convention

I ignored these details because they’re unnecessary distractions from seeing how information flows from the jump button into the rest of the game. They’re unnecessary because they’re still just programming language conventions, not hard truths about how a jump button must work.

Sonic’s motion could be in its own thread—everything could be in its own thread. Iterating through independent motion updates in a main loop produces the same result as running many synchronized loops in parallel. Sure, that independence is essential and famously difficult to achieve and maintain in a language like C. But concurrent loops will never implicitly affect each other in a language that does not express implicit effects.

Years ago I would joke about writing a new programming language to solve a problem. Now I realize it’s no joke. I’m often trying to express a precise message to the computer that has no clear expression in the language I’m using. As a beginning programmer I always interpreted that as my message being wrong. But it’s incidental, a constraint of the existing system not covering the design. Sometimes you have to suck it up and hack, but not because your better intentions are unrealistic. You’re bound to think that they are if you can’t visualize how a better program could work.

☙

A better program

Imagine a script for Sonic akin to the outer while block of the two-loop program. However, each line represents an activity that lasts several seconds, as in a real script that an actor follows. When the activity is over, the next one begins.

The first line of Sonic’s script says: move on the ground until you jump, starting from an initial location x0 and velocity s0 and returning your final location p1 and velocity v1. ³

motion x0 s0 = do   (p1, v1) <- in2D (until jump (groundMotion x0 s0))

The next line computes the initial velocity after jumping, which is just the final ground velocity but with its vertical component set to jumpImpulse.

                    let v1' = v1 { getY = jumpImpulse }

With that in hand, the following line says: move in the air until you land, starting from initial location p1 and velocity v1' and returning your final location p2 and velocity v2.

                    (p2, v2) <- until land (airMotion p1 v1')

Lastly, the script calls itself to say: do this whole thing again starting from the latest location and velocity.

                    motion (getX p2) (getX v2)

How do you like that? It says exactly what we’ve been talking about, but it lacks anything like a while loop to imply that it blocks execution of other code. Other features of the game are expressions independent of this one. These all have meaningful values on their own, and composing them need not define a particular flow of control. That’s the perspective of lazy functional programming and Haskell, the lazy language we’re using. Both are pretty foreign if you’re used to the descendants of C, and this program might look even more fictional than the last one. On the contrary, it is more realistic.

From loops to signal processors

What are until and jump besides rarefied pseudocode? They appear to impose some external interrupt condition on the call to the procedure groundMotion. But groundMotion is not a procedure. Instead, it is a signal function.

We can very roughly compare a signal function to the body of a loop. It generates a set of outputs from a set of inputs, each one corresponding to a moment in time. These sets are signals carrying different values at different times, and a signal function transforms one signal into another. We treat each signal as a unit—instead of iteratively assigning new values to variables, a signal function simply has an output signal. Other signal functions take that signal as input. Chaining signal functions together in this way gives a new, composite signal function that represents the whole chain.

A signal is the totality of all the values it ever carries. This is important, because if we write in terms of total signals rather than their momentary values, our code no longer has different meanings at different times. The passage of time is not an effect of executing the code that a programmer must infer. Instead, the code says explicitly how time will pass. This is defined solidly and precisely enough to constitute a language unto itself, so signal function expressions have a special syntax.

Loops repeat themselves but may evolve with each repetition, and so too may a signal function’s input-output transformation evolve over time. Theoretically, this happens because of a feedback signal: the output signal is delayed and routed back as an input signal. A prime example of this evolution is a signal function that switches between different modes of operation. Given some signal that represents a timeline of events, such a signal function transforms its input in two different ways: one way before the first event occurrence, and another way afterward.

Scripting the signal function

Coding a switch is particularly easy using until. It takes as arguments two signal functions: one that represents the first mode, and one that puts out a timeline of termination events. Together these mean, behave as a certain signal function until a certain event occurs. That is, we use until to express an activity that can appear in sequence with others to form a script like motion. The script concatenates several signal functions into one big signal function that, as time goes by, switches its behavior from one to the next.

The single signal function that switches between different modes is one that defines Sonic’s motion. Its input signals are the state of the directional pad and of the jump button, and its output signals are Sonic’s location and velocity. It transforms the controller state into the motion state in two modes, one for the ground and one for the air. Hence the signal functions airMotion and groundMotion. Each of them expresses the same thing that our loops did without the single-threaded baggage. And yet they’re just values that can be arguments to a function like until. ⁴

The other argument to until is a signal function like jump, and it operates on different signals. Its output signal is a timeline of activity-terminating events. Its input signals include not only the controller signals dpad and trigger, but also the activity’s output signals—the output signals of airMotion or groundMotion.

In the case of groundMotion, this is the horizontal location x and speed s. The definition of jump therefore begins by declaring these terms as input signals.

jump = proc ((dpad, trigger), (x, s)) -> do

The signal trigger is the input to edge, which detects a rising edge in a Boolean signal.

           done <- edge -< trigger

The output of edge is a signal done, a timeline of rising-edge events. At the moment the value of trigger changes from False to True, done carries a value denoting an event occurrence. This becomes the output signal of jump, after receiving an extra tag value recording the current motion state (x, s).

           returnA -< tag done (x, s)

At the moment of termination, this current motion state is in fact the final motion state on the ground, which is the return value in the first line of motion. The tagged event timeline informs until of the moment it should switch to the next line and provides the value that it should return when it does.

So jump terminates groundMotion. In much the same way, land terminates airMotion. Here the input signal to edge depends not on the dpad or trigger, but the output signals p and v of airMotion. That reflects the fact that motion in the air ends only when Sonic’s motion leads him to the ground, not when controller state changes.

land = proc ((dpad, trigger), (p, v)) -> do
           done <- edge -< getY p <= ground (getX p)
           returnA -< tag done (p, v)

In this program, then, the jump button gates the switch from the ground-motion signal function to the air-motion signal function. The information flow from the jump button to the switching mechanism is plainly expressed in the language we have used. It is more explicit here than in the two-loop program, which relies on loops and returns and threads implicit in the language that don’t really work the way we want. Haskell lets us instead develop our own control mechanisms that precisely reflect our intentions.

☙

The information

Clearly there are many possible implementations of a jump button. We’ve looked at three styles that all work differently, and there are many others out in the wild. There’s a common thread to all of them, though.

As I’ve mentioned a few times, they are all are ways of transmitting the jump button’s information and transforming it into a shift from what we see on the ground to what we see in the air. A crucial element of the information is when the button is pressed, which must be the same moment that the shift occurs. The causal relationship between the button and the game’s observable behavior is the transmission of this time information. Only by a faithful transmission does the button make Sonic jump. We interpret that as causation because the moment of the shift is tightly correlated with the moment of the button press. If knowing the former lets us easily predict the latter, then we say that the button controls the game. If instead that prediction is difficult, then we say that the button has no control.

Because the last program is based on signal functions, timing is explicit in the meanings of its terms. In contrast, timing is implied in the other programs only as the time it takes to execute each statement. Signal functions also make information flow explicit in the form of signal chains—precisely related, mathematical terms for the button state and the game’s observable behavior. The other programs define the information flow as the order in which the computer executes assignments. The assignments can appear anywhere, subject to arbitrary conditions.

That’s why I call the last program a better program. The script motion directly encodes the shift as two separate lines: when the first is done, the second begins. To provide the when, jump literally points the way from trigger to done. It is manifest how the information flows and how it becomes the shift from one mode to the next.

Now Sonic can become Super Sonic

In the sequel to Sonic the Hedgehog, Sonic can become Super Sonic after collecting all seven Chaos Emeralds. Super Sonic is invincible, incredibly fast and agile, and looks totally rad. But getting the Chaos Emeralds is challenging, and I will never forget my tears of fury after repeatedly failing the later trials.

When I finally got the last Emerald, I was speechless. The screen said in no uncertain terms: NOW SONIC CAN BECOME SUPER SONIC. And it was rad. To my mind, so thoroughly steeped in the rules of the game, this was tantamount to gaining a bona fide super power. I was so fast, I could jump anywhere, and I bulldozed through enemies without a scratch.

There were still limits. I could get crushed or fall down a bottomless pit, and the rings that I collected gradually vanished until they ran out, turning Super Sonic back into regular Sonic. I could still lose the game, but now I had more options for winning.

Since then, I’ve wrapped my mind around programming several times trying to get a satisfying perspective on what as simple a thing as a jump button really requires. I thought I learned the rules, but my programs still had bugs. They became complex in unexpected ways. Despite tons of reading, experimenting, and conversations with peers, I only learned occasional lessons about why that is and whether I could overcome it. That has frustrated me for a long time.

Now I have some answers to my irritating questions. The jump button can work many different ways, but they all accomplish the same essential task of conveying and transforming information about time. There are many ways to express this, and an existing system’s constraints on the expression may seem like laws when they are actually conventions. Perspectives like this offer us more options. It gave me, for example, an efficient way to do something I thought I’d never accomplish. Not quite invincibility, super speed, and flashing yellow hair all at once, but I’ll take it.

Further reading:

• The Yampa Arcade
  by Antony Courtney and Henrik Nilsson
• Functional Reactive Programming, Continued
  by Henrik Nilsson, Antony Courtney, and John Peterson
• Functional Reactive Animation
  by Conal Elliott and Paul Hudak
• Structure and Interpretation of Computer Programs
  by Hal Abelson and Gerald Sussman, with Julie Sussman
• Object Oriented Game Programming: The Scripted Event System
  by Paul Stevens
• Game Programming Patterns
  by Robert Nystrom
• Game Coding Complete
  by Mike McShaffry and David Graham

Other articles by Alex Stuart